
Who was the smartest of the smarties? Gauss? Young? Einstein? Dirac? Witten? Smolin? Of ALL time? How about Nick Bourbaki? It's been said he had the power of 15 fine minds.
If he were alive today, would Peter Woit let him post on Not Even Wrong, or moderate him heavily? A mystery!
From Wikipedia:
Nicolas Bourbaki is the collective pseudonym under which a group of (mainly French) 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality. Their work led to the discovery of several concepts and terminologies still discussed.
While Nicolas Bourbaki is an invented personage, the Bourbaki group is officially known as the Association des collaborateurs de Nicolas Bourbaki (Association of Collaborators of Nicolas Bourbaki), which has an office at the École Normale Supérieure in Paris.
Books by Bourbaki
Aiming at a completely self-contained treatment of the core areas of modern mathematics based on set theory, the group produced the Elements of Mathematics (Éléments de mathématique) series, which contains the following volumes (with the original French titles in parentheses):
- Set theory (Théorie des ensembles)
- Algebra (Algèbre)
- Topology (Topologie générale)
- Functions of one real variable (Fonctions d'une variable réelle)
- Topological vector spaces (Espaces vectoriels topologiques)
- Integration (Intégration)
and later
- Commutative algebra (Algèbre commutative)
- Lie groups (Groupes et algèbres de Lie)
- Spectral theory (Théories spectrales)
The book Variétés différentielles et analytiques was a fascicule de résultats, that is, a summary of results, on the theory of manifolds, rather than a worked-out exposition. A final volume IX on spectral theory (Théories spectrales) from 1983 marked the presumed end of the publishing project; but a further commutative algebra fascicle was produced in 1998.
While several of Bourbaki's books have become standard references in their fields, some have felt that the austere presentation makes them unsuitable as textbooks.[1] The books' influence may have been at its strongest when few other graduate-level texts in current pure mathematics were available, between 1950 and 1960.[2]
Notations introduced by Bourbaki include the symbol 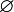 for the empty set and a dangerous bend symbol, and the terms injective, surjective, and bijective.
for the empty set and a dangerous bend symbol, and the terms injective, surjective, and bijective.
It is frequently claimed[by whom?] that the use of the blackboard bold letters for the various sets of numbers was first introduced by the group. There are several reasons to doubt this claim.[3]
Influence on mathematics in general
The emphasis on rigour may be seen as a reaction to the work of Henri Poincaré,[4] who stressed the importance of free-flowing mathematical intuition, at a cost of completeness in presentation. The impact of Bourbaki's work initially was great on many active research mathematicians world-wide.
It provoked some hostility, too, mostly on the side of classical analysts; they approved of rigour but not of high abstraction. Around 1950, also, some parts of geometry were still not fully axiomatic — in less prominent developments, one way or another, these were brought into line with the new foundational standards, or quietly dropped. This undoubtedly led to a gulf with the way theoretical physics is practiced.[5]
Bourbaki's direct influence has decreased over time.[5] This is partly because certain concepts which are now important, such as the machinery of category theory, are not covered in the treatise. The completely uniform and essentially linear referential structure of the books became difficult to apply to areas closer to current research than the already mature ones treated in the published books, and thus publishing activity diminished significantly from the 1970s.[6] It also mattered that, while especially algebraic structures can be naturally defined in Bourbaki's terms, there are areas where the Bourbaki approach was less straightforward to apply.[citation needed]
On the other hand, the approach and rigour advocated by Bourbaki have permeated the current mathematical practices to such extent that the task undertaken was completed.[7] This is particularly true for the less applied parts of mathematics.
The Bourbaki seminar series founded in post-WWII Paris continues. It is an important source of survey articles, written in a prescribed, careful style. The idea is that the presentation should be on the level of absolute specialists, but for an audience which is not specialized in the particular field.
The group
Accounts of the early days vary, but original documents have now come to light. The founding members were all connected to the Ecole Normale Supérieure in Paris and included Henri Cartan, Claude Chevalley, Jean Coulomb, Jean Delsarte, Jean Dieudonné, Charles Ehresmann, René de Possel, Szolem Mandelbrojt and André Weil. There was a preliminary meeting, towards the end of 1934.[8] Jean Leray and Paul Dubreil were present at the preliminary meeting but dropped out before the group actually formed. Other notable participants in later days were Laurent Schwartz, Jean-Pierre Serre, Alexander Grothendieck, Samuel Eilenberg, Serge Lang and Roger Godement.
The original goal of the group had been to compile an improved mathematical analysis text; it was soon decided that a more comprehensive treatment of all of mathematics was necessary. There was no official status of membership, and at the time the group was quite secretive and also fond of supplying disinformation. Regular meetings were scheduled, during which the whole group would discuss vigorously every proposed line of every book. Members had to resign by age 50.[9]
The atmosphere in the group can be illustrated by an anecdote told by Laurent Schwartz. Dieudonné regularly and spectacularly threatened to resign unless topics were treated in their logical order, and after a while others played on this for a joke. Godement's wife wanted to see Dieudonné announcing his resignation, and so on one occasion while she was there Schwartz deliberately brought up again the question of permuting the order in which measure theory and topological vector spaces were to be handled, to precipitate a guaranteed crisis.
The name "Bourbaki" refers to a French general Charles Denis Bourbaki;[10] it was adopted by the group as a reference to a student anecdote about a hoax mathematical lecture, and also possibly to a statue. It was certainly a reference to Greek mathematics, Bourbaki being of Greek extraction. It is a valid reading to take the name as implying a transplantation of the tradition of Euclid to a France of the 1930s, with soured expectations.[11]
Appraisal of the Bourbaki perspective
The underlying drive, in Weil and Chevalley at least, was the perceived need for French mathematics to absorb the best ideas of the Göttingen school, particularly Hilbert and the modern algebra school of Emmy Noether, Artin and van der Waerden. It is fairly clear that the Bourbaki point of view, while encyclopedic, was never intended as neutral. Quite the opposite: it was more a question of trying to make a consistent whole out of some enthusiasms, for example for Hilbert's legacy, with emphasis on formalism and axiomatics. But always through a transforming process of reception and selection — their ability to sustain this collective, critical approach has been described as "something unusual".[12]
The following is a list of some of the criticisms commonly made of the Bourbaki approach:[13]
Furthermore, Bourbaki make no use of pictures in their presentation.[19] In general, Bourbaki has been criticized for reducing geometry as a whole to abstract algebra and soft analysis.[20]
Dieudonné as speaker for Bourbaki
Public discussion of, and justification for, Bourbaki's thoughts has in general been through Jean Dieudonné (who initially was the 'scribe' of the group) writing under his own name. In a survey of le choix bourbachique written in 1977, he did not shy away from a hierarchical development of the 'important' mathematics of the time.
He also wrote extensively under his own name: nine volumes on analysis, perhaps in belated fulfillment of the original project or pretext; and also on other topics mostly connected with algebraic geometry. While Dieudonné could reasonably speak on Bourbaki's encyclopedic tendency, and tradition (after innumerable frank tais-toi, Dieudonné! ("Hush, Dieudonné!") remarks at the meetings), it may be doubted whether all others agreed with him about mathematical writing and research. In particular Serre has often championed greater attention to problem-solving, within number theory especially, not an area treated in the main Bourbaki texts.
Dieudonné stated the view that most workers in mathematics were doing ground-clearing work, in order that a future Riemann could find the way ahead intuitively open. He pointed to the way the axiomatic method can be used as a tool for problem-solving, for example by Alexander Grothendieck. Others found him too close to Grothendieck to be an unbiased observer. Comments in Pal Turán's 1970 speech on the award of a Fields Medal to Alan Baker about theory-building and problem-solving were a reply from the traditionalist camp at the next opportunity[21][not in citation given], Grothendieck having received the previous Fields Medal in absentia in 1966.
Bourbaki's influence on mathematics education
In the longer term, the manifesto of Bourbaki has had a definite and deep influence. In secondary education the new math movement corresponded to teachers influenced by Bourbaki. In France the change was secured by the Lichnerowicz Commission.[22]
The influence on graduate education in pure mathematics is perhaps most noticeable in the treatment now current of Lie groups and Lie algebras. Dieudonné at one point said 'one can do nothing serious without them', for which he was reproached; but the change in Lie theory to its everyday usage owes much to the type of exposition Bourbaki championed. Beforehand Jacques Hadamard despaired of ever getting a clear idea of it.
See also
Notes
- ^ Confronted by the task of appraising a book by N. Bourbaki, this reviewer feels as if he were required to climb the Nordwand of the Eiger. The presentation is austere and monolithic. The route is beset by scores of definitions, many of them apparently unmotivated. Always there are hordes of exercises to be worked through painfully. One must be prepared to make constant cross-references to the author's many other works. Hewitt, Edwin (1956). "Review: Espaces vectoriels topologiques". Bulletin of the American Mathematical Society 62: 507–508. doi:10.1090/S0002-9904-1956-10042-6. [1]
- ^ ...by 1958 when the original six books were completed, the first few of these books were already almost 20 years out of date. [2]
- ^ (1) the symbols do not appear in Bourbaki publications (rather, ordinary bold is used) at or near the era when they began to be used elsewhere, for instance, in typewritten lecture notes from Princeton University (achieved in some cases by overstriking R or C with I), and (an apparent first) typeset in Gunning and Rossi's textbook on several complex variables;[citation needed] (2) Jean-Pierre Serre, a member of the Bourbaki group, has publicly inveighed against the use of "blackboard bold" anywhere other than on a blackboard.[citation needed]
- ^ Bourbaki came to terms with Poincaré only after a long struggle. When I joined the group in the fifties it was not the fashion to value Poincaré at all. He was old-fashioned. Pierre Cartier interviewed by Marjorie Senechall. "The Continuing Silence of Bourbaki". Mathematical Intelligencer 19: 22–28. 1998. [3]
- ^ a b Ian Stewart: Mathematicians knew how to decode Bourbakist messages, but the rest of the world didn't. This led to unfortunate misunderstandings, and by the end of the sixties, mathematics and physics departments were no longer on speaking terms. Ian Stewart (11 1995). "Bye-Bye Bourbaki: Paradigm Shifts in Mathematics". The Mathematical Gazette (The Mathematical Association) 79 (486): 496–498. doi:10.2307/3618076. http://jstor.org/stable/3618076.
- ^ Borel (1998)
- ^ Chevalley in Guedj (1985)
- ^ The minutes are in the Bourbaki archives — for a full description of the initial meeting consult Liliane Beaulieu in the Mathematical Intelligencer.
- ^ This resulted in a complete change of personnel by 1958; see Robert Mainard paper cited below. However, the Aubin paper cited below quotes the historian Liliane Beaulieu as never having found written affirmation of this rule.
- ^ Charles Denis Bourbaki fought in the Crimean War and Franco-Prussian War, refer to A. Weil: The Apprenticeship of a Mathematician, Birkhäuser Verlag 1992, pp 93-122.
- ^ It is said that Weil's wife Evelyne supplied Nicolas. (Mentioned by McCleary (PDF). This is more or less confirmed by Robert Mainard((PDF), a long article in French, which gives numerous further details: why N?, and the prank lecture of Raoul Husson in a false beard that gave rise to Bourbaki's theorem). They married in 1937, she having previously been with de Possel; who then unsurprisingly left the group.
- ^ Hector C. Sabelli, Louis H. Kauffman, BIOS (2005), p. 423.
- ^ Pierre Cartier, a Bourbaki member 1955–1983, comments explicitly on several of these points (The Continuing Silence of Bourbaki, article from the Mathematical Intelligencer): ...essentially no analysis beyond the foundations: nothing about partial differential equations, nothing about probability. There is also nothing about combinatorics, nothing about algebraic topology, nothing about concrete geometry. And Bourbaki never seriously considered logic. Dieudonné himself was very vocal against logic. Anything connected with mathematical physics is totally absent from Bourbaki's text.
- ^ This is one of the reasons for diminishing influence: Le développement des mathématiques dites appliquées, de la statistique et des probabilités, des théories liées à l'informatique a diminué l'influence de Bourbaki[4]
- ^ Tim Gowers discusses at length the distinction between mathematicians who regard their central aim as being to solve problems, and those who are more concerned with building and understanding theories in his The Two Cultures of Mathematics (PDF).
- ^ Lennart Carleson spoke of this in an interview (Infomat August 2006 (PDF)): ...that book [from 1968] was written mostly as a way to encourage the teachers to stay with established values. That was during the Bourbaki and New Math period and mathematics was really going to pieces, I think. The teachers were very worried and they had very little backing.
- ^ Heinz König: The traditional abstract measure theory which emerged from the achievements of Borel and Lebesgue in the first two decades of the 20th century is burdened with its total limitation to sequential procedures and its neglect of regularity. The alternative theory due to Bourbaki which arose in the middle of the century was able to relieve these burdens, but produced new ones. In particular its fundamental turn to inner regularity, based on the profound role of compactness, was done with the inappropriate weapons from the outer arsenal, which subsequently enforced that unfortunate construction named the essential one. All this produced serious obstacles against a unified theory of measure and integration, for example for the notion of signed measures, the formation of products and for the representation theorems of Daniell-Stone and Riesz types.[5]
- ^ Discussed by the set theorist Adrian Mathias (The Ignorance of Bourbaki (PDF)). See also Mashaal (2006), p.120, "Lack of interest in foundations".
- ^ Pierre Cartier, in the article cited above, is quoted as later saying The Bourbaki were Puritans, and Puritans are strongly opposed to pictorial representations of truths of their faith.
- ^ In the French context it has been said that geometry was in effect exiled from secondary teaching: Pour ce qui est des années 1960, l’effet de la réforme dite des mathématiques modernes sur l’enseignement de la géométrie est bien connu : si Dieudonné, comme Bourlet finalement, lance "A bas Euclide", le résultat n’est pas l’élaboration d’une géométrie plus expérimentale, plus intuitive. C’est l’effacement de la géométrie derrière l’algèbre linéaire et la quasi-disparition de l’enseignement de la géométrie élémentaire au collège et au lycée pour une dizaine d’années.—"As for the 1960s, the effect of this reform of modern mathematics on the teaching of geometry is well-known: if Dieudonné, like Bourlet finally, says "push Euclid back," the result is not the development of a geometry that is more experimental, more intuitive. It's the erasure of geometry behind linear algebra, and the quasi-disappearance of the teaching of elementary geometry in high school, for ten years."[6]
- ^ On the Work of Alan Baker
- ^ Mashaal (2006) Ch.10: New Math in the Classroom
References
External links
 The Downside of Anti-Gravity
The Downside of Anti-Gravity Engineer's View of Men and Women
Engineer's View of Men and Women






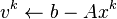
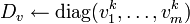

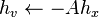
 then
then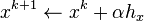



 Pictured above: T.O.E. Venn Diagtam
Pictured above: T.O.E. Venn Diagtam
 The New York Giants' defense has knocked 7 quarterbacks out of the game in 7 weeks. This is their latest victim, Tony Romo of the Dallas Cowboys. Up next after a bye: Matt Hasselback of the Seattle Seahawks. Check that life insurance policy, Matt.
The New York Giants' defense has knocked 7 quarterbacks out of the game in 7 weeks. This is their latest victim, Tony Romo of the Dallas Cowboys. Up next after a bye: Matt Hasselback of the Seattle Seahawks. Check that life insurance policy, Matt.















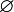 for the
for the